Detecting epistasis in human complex traits
Dec 30, 2017 10:30 · 1761 words · 9 minutes read
\[ \newcommand\E{\text{E}} \newcommand\nocr{\nonumber\\} \newcommand\var{\text{Var}} \newcommand\logit{\text{logit}} \]
Meta data of reading
- Journal: Nature Review Genetics
- Year: 2014
- DOI: 10.1038/nrg3747
Motivation
Under GWAS framework, the causal variants are found with independent with additive and cumulative effects. But such assumption is arguably unrealistic. So it is necessary to consider the case where variants do not act independently (genetic interaction, epistasis). In this review, the authors refer:
- Functional effect: The general observation that effect of a particular variant depends on the genotype of another variant
- Statistical effect: The interaction variance that can be explained by a combination of causal variants that is not due to their independent effects (namely, \(1 + 1 \ne 2\))
, where epistasis is referred to statistical effect.
The authors point out that the presence of functional epistasis does not automatically imply the presence of substantial statistical epistasis and vice versa. By considering epistasis or not, there are two types of heritability:
- Narrow-sense heritability (\(h^2\)): The estimated proportion of the phenotypic variance of a trait that is attributable to independent, additive genetic effects
- Broad-sense heritability (\(H^2\)): The estimated proportion of the phenotypic variance of a trait that is attributable to all additive and non-additive genetic effects
The authors point out the reason why epistasis is often under debate (its importance). There are two major goals of GWAS:
- Identify causal variants of a particular trait to understand underlying biology
- Estimate the effects of causal variants to predict phenotypic outcomes
Functional epistasis can benefit the first goal and statistical epistasis can benefit the second goal.
This paper surveys the methodology and software of the detection of epistasis along with the latest empirical evidence for the importance of epistasis and potential utility in searching for genetic interaction.
Methods for detecting epistasis
There have been methods developed to detect whether two or more loci differs from that predicted by their individual effects. Most methods use SNPs for pairwise or higher-order interactions in GWAS data. There are two strategies:
- Hypothesis-free: Namely exhaustive search. Test for all possible combinations in all SNPs which involves billions of tests. It is both computationally expensive and statistically challenging
- Hypothesis-driven: Test for a subset of SNPs and/or epistasis
Regression-based method
The idea is to compare the saturated model (\(L_{S}\)) and reduced model (\(L_R\)) (considering interaction term between SNPs or not). For instance, in case-control study, \(L_S\) can be:
\[\begin{align} \logit(Pr(Y = 1)) &= \alpha + \beta x_1 + \gamma x_2 + \delta x_1 x_2 \nonumber \end{align}\], where \(x_1, x_2\) are binary variables and \(\delta\) can be parameterized by four numbers according to the four possible configuration of \(x_1, x_2\).
Several progresses have been made to overcome the computational load. First, advanced data structure and parallelization have been introduced. Second, approximate tests have been applied, such as F ratio and Kirkwood superposition approximation (for \(L_S\) versus \(L_R\) tests under the assumption of HWE).
Although the hypothesis-free regression-based methods have become computationally tractable, they still suffer from low power (needs big sample size). Therefore, the practical compromise is to focus on the SNPs with genome-wide association signal. Moreover, the power of the test is a function of: i) interaction effect size; ii) sample size; iii) linkage disquilibrium. So, dense marker data can benefit the analysis as well.
LD- and haplotype-based methods
The idea is to test whether the co-occurrence of SNPs is enriched in cases relative to controls. It is computationally faster and statistically more powerful than regression-based methods. It works well for unlinked loci in rare diseases.
For instance, the LD of the pair of SNPs can be compared for cases and controls to see if the difference is significant (LD-based method). Haplotype-based methods adapted from LD-based one with equal power. With GWAS data, the linkage phase should be inferred before performing this test.
LD-based methods may generate inflated false positives because HWE does not always hold genome-wide. In LD-based method, a Z-score statistic is used from the difference in Pearson correlation in cases and controls. But simulation suggests that Z-score is inflated when two SNPs are highly correlated and/or both have significant marginal effects.
Haplotype-based methods incorporates a weighted average of the joint effects of two SNPs can control false positives when only one SNPs has marginal effects. This limitation can be overcome by using full logistic regression model (also with correction of covariates). So, a two-step approach where i) genome-wide screening with Z-score statistic (high power); ii) regression-based model to test the most promising interactions (low false positives).
Bayesian methods
The idea is to compute the posterior probability for the SNP to be i) unassociated; ii) associated by marginal effect; iii) associated by joint effect. Combining Bayesian framework and GLM allows tests of SNP interactions with the consideration of covariates, marginal effect, and gene-environment interaction. Also, Bayesian approach can average multiple models when the underlying interaction patterns are unknown.
Data-filtering methods
Variance heterogeneity refers to the case where for a single bi-allelic SNP, the three genotypes have difference conditional phenotic variance. It can be used to select potentially interacting SNPs (since variance heterogeneity is a necessary condition for genetic interaction). But it suffers limited detectable variance heterogeneity.The cautions are:
- Biases introduced by algorithm
- Publication bias in existing knowledge
- Context dependence
- Filtering threshold may change the null distribution of test statistic
Artificial intelligence algorithms
…
Group- and module-based methods
The idea is to group SNPs into functional modules before performing tests, which can substantially reduce the statistical burden. A common practice is to group SNPs by gene and derive gene-based variable that factors in SNP-based correlations for regression-based methods or for analogues LD-based approaches. Another strategy is to compute pairwise interactions between groups and derive gene-based interaction p-value by integrating all pairwise p-values. Additionally, with pairwise interaction statistics between groups along with marginal effects, the gene-gene interaction can be analyzed using network analysis algorithms (SNPrank).
The authors point out that such gene-based method benefits from imputed genotypes from external LD information since it may capture unobserved causal variant. The implicit assumption behind gene-based method is “no intragenic interaction”.
Multitrait and multilevel integration
Pleiotropic epistasis is statical interaction signals shared in multiple traits. It can be identified by looking for SNP-SNP interaction that are shared across multiple traits or introducing composed “trait” (combining multiple traits) as latent variable in Bayesian framework. For example, a BEAM-derived method uses three latent variables: gene expression, SNPs, and individuals.
Summary and future directions
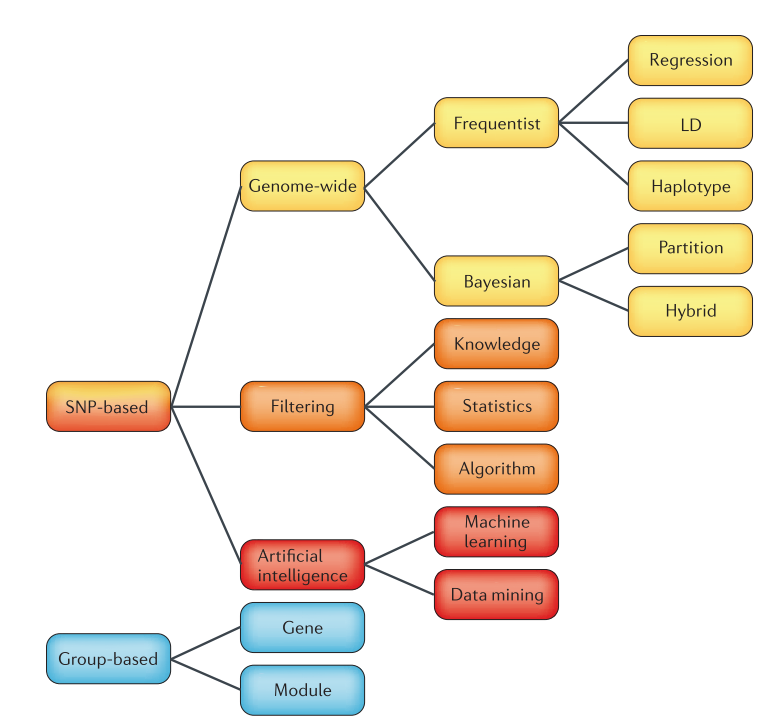
Summary of reviewed methods for detecting epistasis
All methods mentioned above take genotyped SNPs and they cannot handle imputed SNPs with uncertainty. But this is useful in meta-analysis of epistasis which needs to be developed. Current methods do not consider sex chromosome.
Overview of empirical evidence for epistasis
Hypothesis-free studies
People have done genome-wide epistasis scanning using WTCCC data. It turns out that the majority of the statistical interactions were in MHC region affecting T2D or RA. Such signals may be caused by haplotype effects where statistical interaction pair together tags a causal variant in proximity.
The result also indicated that many epistasis effect has multiplicative pattern, namely the effect of marginal additive term is bigger than the expected, and such effect can be removed by changing the scale of the trait measured (scale effect).
But scale effect happens in two marginally non-significant SNPs, which indicates that epistasis analysis may increase the power of marginal effect analysis. It is possible when two SNPs has small effect but their interaction term has big effect. Taking this idea, researchers used additive \(\times\) additive model to scan the genome and identified similar results as the above one.
For traits as gene expression which have bigger genetic effect, researchers used BSGS data and identified 501 epistasis effect in discovery stage but only 30 could be replicated. The issue came from the unobserved causal variants (as discussed previously), which can drive the epistasis signal. The problem cannot be fixed even after filtering on LD. One important conclusion was that even corrected for power the attributable additive effects was still far more bigger than non-additive ones. The authors thought that since the current studies show few evidence of replicated non-additive effects in genome-wide analysis, the non-additive effect with large effect size is unlikely to exist.
Hypothesis-driven studies
The hypothesis-driven studies can reduce the statistical burden substantially. The authors point out that the hypothesis-driven results also suffer from lack of replication.
The authors list several successful examples. In Alzheimer’s disease, FYN and RNF219 decrease the risk only if APOE4 mutant exists. Here the strategy is to limit the search to genetic effect that affects endophenotypes. Endophenotype is referred as the heritable traits that are genetically correlated with disease traits. They are often traits (such as the level of a metabolite or transcript) that can be measured in all individuals (both diseased and healthy) and that can potentially provide a predictor of disease status.
Two interacting SNPs in HLA-DR2 affects the risk of multiple sclerosis toghether. The epistasis effect has been confirmed experimentally.
Regarding the pattern of interaction. If variant A increases risk only when variant B exists, the underlying mechanism might be that there are two redundant pathways (A in one and B in the other). Another pattern is that variant A increases risk only when variant B absents. It corresponds to the case where A and B are in the same pathway. Therefore, one strategy to propose the testing pairs is to make use of knowledge on biological function.
Alternatively, one can only test on variants with large marginal effect. There are cases where this strategy works. But it can also fail (no significant results for T2D, BMI, serum uric acid levels under current results).
The authors mention the pitfall of the current epistasis studies. They point out that the analysis is done on observed scale and an interaction that is non-additive in observed scale can be addtive in liability scale since even if variants contribute additively, if the disease occurs under some threshold, it appears to be epistasis under current analysis. It turns out that such effect is largest when disease prevalence is small.
Summary
Little evidence of statistical epistasis comparing to additive model and the genetic contribution substantially smaller than the additive one, especially for the case of pairwise epistasis between SNPs. However, hypothesis-driven analysis (based on biological function) is more successful than the genome-wide scanning one . It indicates that functional epistasis does exist. But the current progress has made genome-wide scanning (hypothesis-free tests) easily achievable.
The future direction is to develope meta-analysis method and to consider multilocus epistasis.